This post was released for Issue 16 of Bitcoin Magazine as part of a series of articles about puzzles and games that started with Issue 12.
Packing problems are a class of optimization problems in mathematics that involve attempting to pack objects together into containers. The goal is to either pack a single container as densely as possible or pack all objects using as few containers as possible.
One of my earliest games (Hippos & Crocodiles – 2009) exploits this type of problem. In Hippos & Crocodiles your goal is to place as many animals on an African river as you can and prevent your opponent from doing the same.
Here I present a nice derivative of this game, while introducing a type of puzzle piece that has been around for more than a century: the polyomino, and also the concept of harvesting (picking items already placed on the board).
A polyomino is a plane geometric figure formed by joining one or more equal squares edge to edge. We can create 12 polyominos by joining 5 squares. These shapes are called pentominoes.
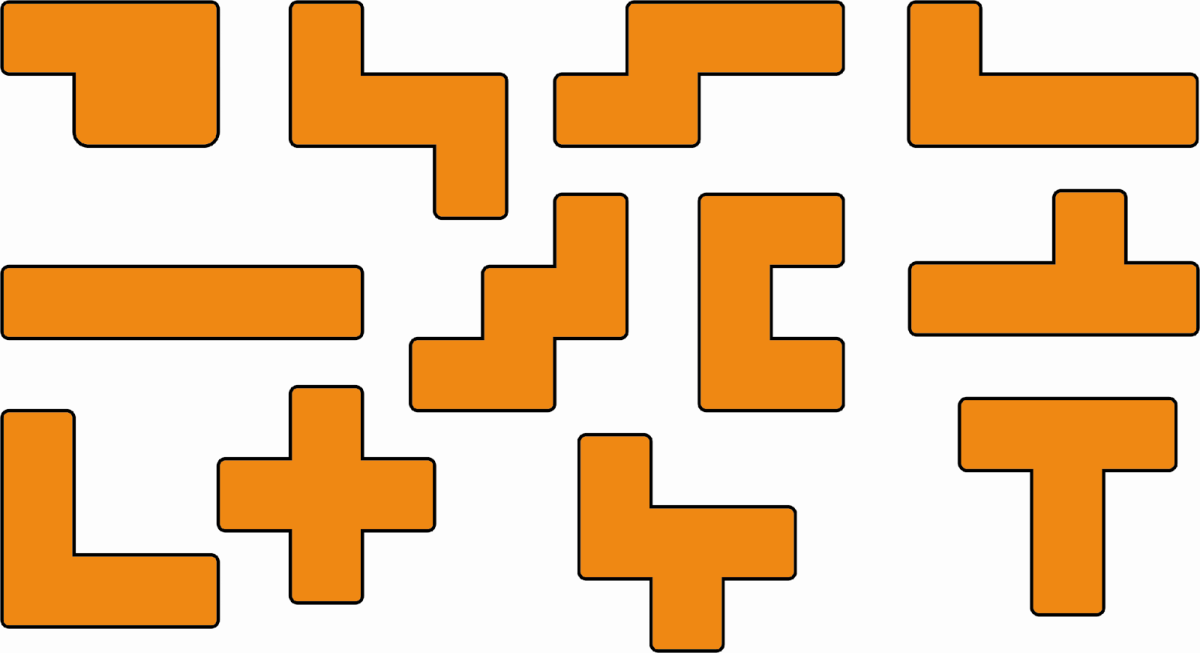
Figure 1: the 12 different pentominoes
There are other sizes of polyominoes (4,6,7…), but the pentomino is the one that works better for this game.
THE GAME: BITCOIN HARVEST
Bitcoin Harvest is a paper-and-pencil game for 2 or more players. Some solitary puzzles can be found at the end of this article, too.
Start by drawing a rectangular grid of any size. 10x10 is recommended for beginners, but for more than 2 players you might need a bigger grid.

Figure 2: the game grid
Secondly, and by turn, each player chooses a pentomino shape. This pentomino will be his ‘harvester’, and the only piece he will use during the game.
Example: Ann chooses the ‘L’, Ben chooses the ‘+’, Claire chooses the ‘U’.

Figure 3: the players’ harvesters (we’re using different colours for clarity)
The player that chose a shape in first place draws two coins in any empty cells of the grid.
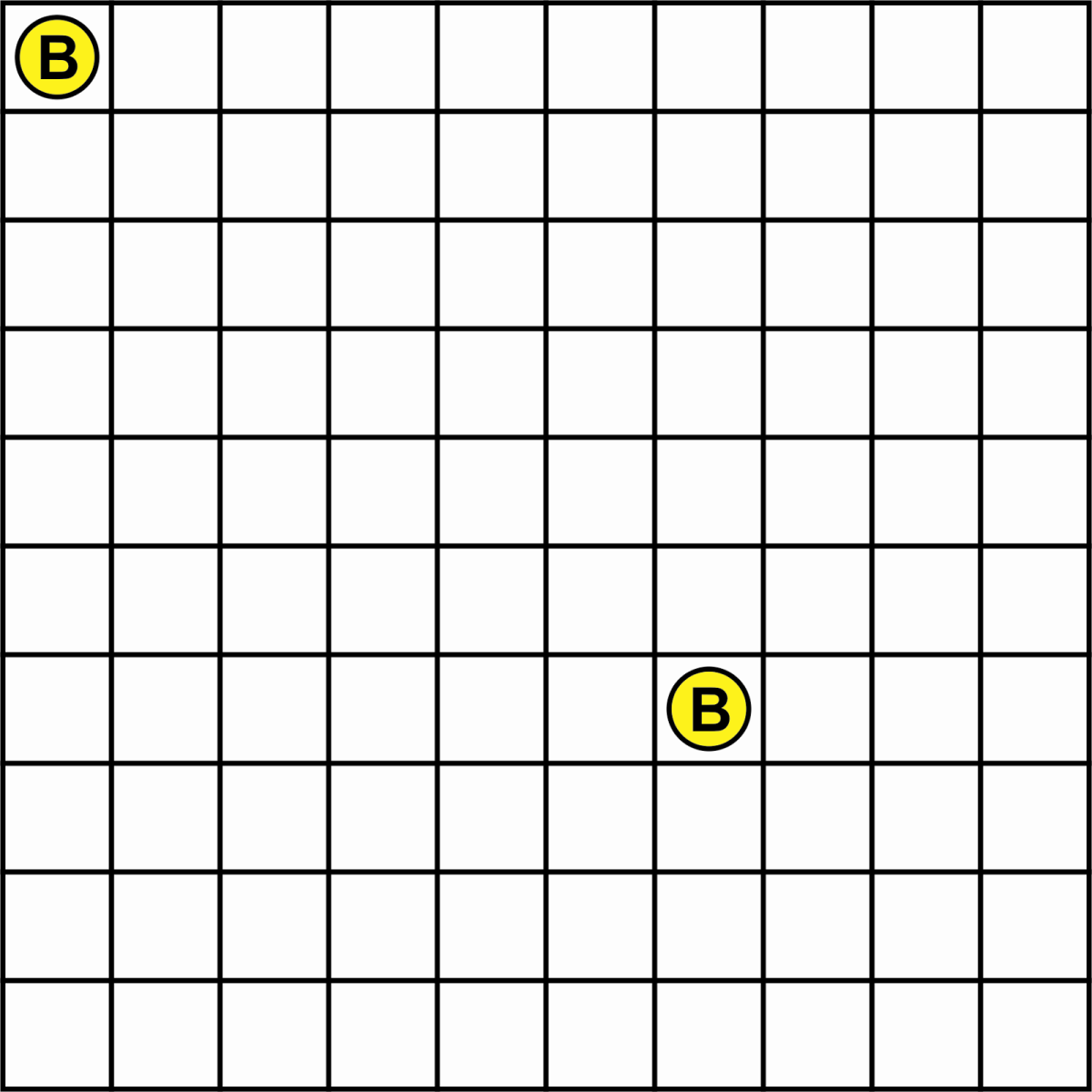
Figure 4: the first player draws two coins
Then, starting with the second player, players take turns doing the following:
- Draw your harvester on the board, so it doesn’t overlap other previously drawn pentominos and no parts of it land outside the board. You can (and should) draw it so it overlaps some coins. Notice that you can draw it rotated or mirrored, as long as it fits with the grid.
- Score as many coins as the pentomino has covered.
- Draw another 2 coins in any two empty spaces (not occupied by coins or pentominoes).
- Pass your turn to the next player.
- If you’re not capable of legally drawing a pentomino (no room for it) you must pass your turn. If all players pass in succession the game ends. The player with the highest score wins.
Here are a few examples of turns:
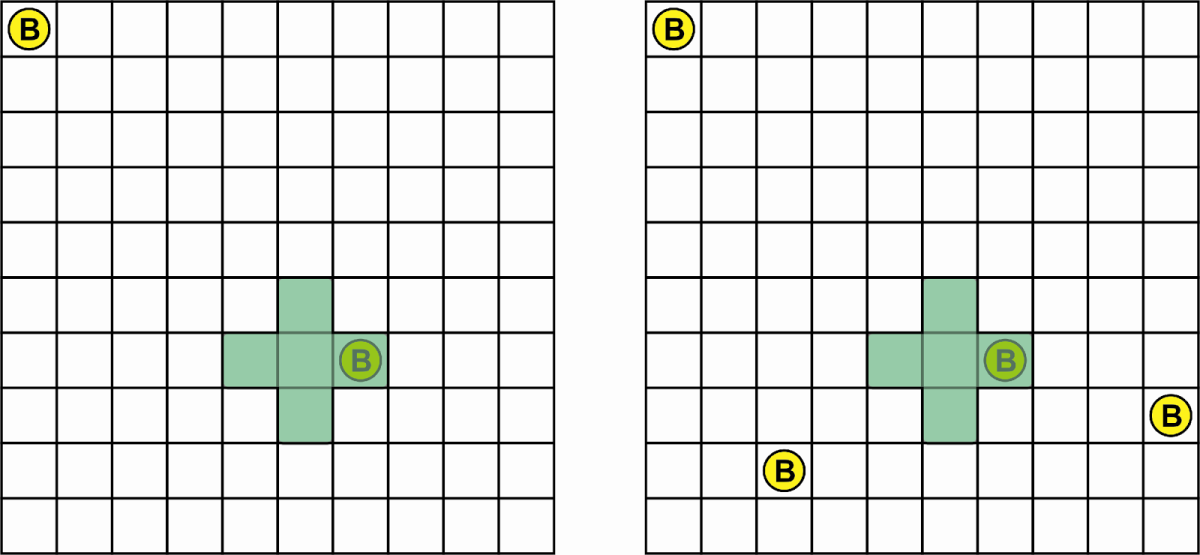
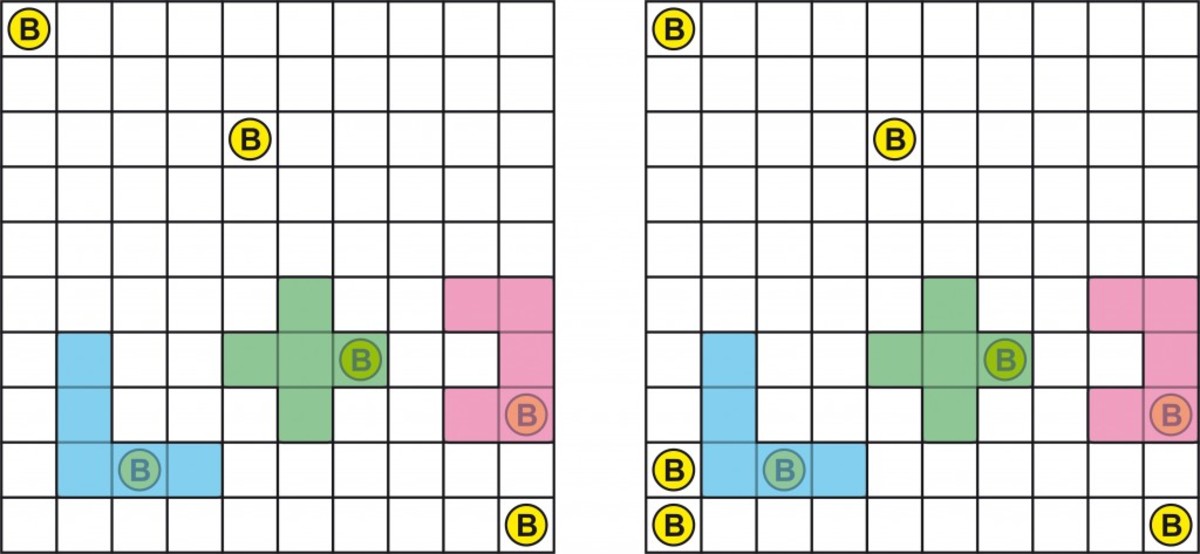
Figure 5: Ben draws his harvester collecting 1 coin, then draws two more coins.
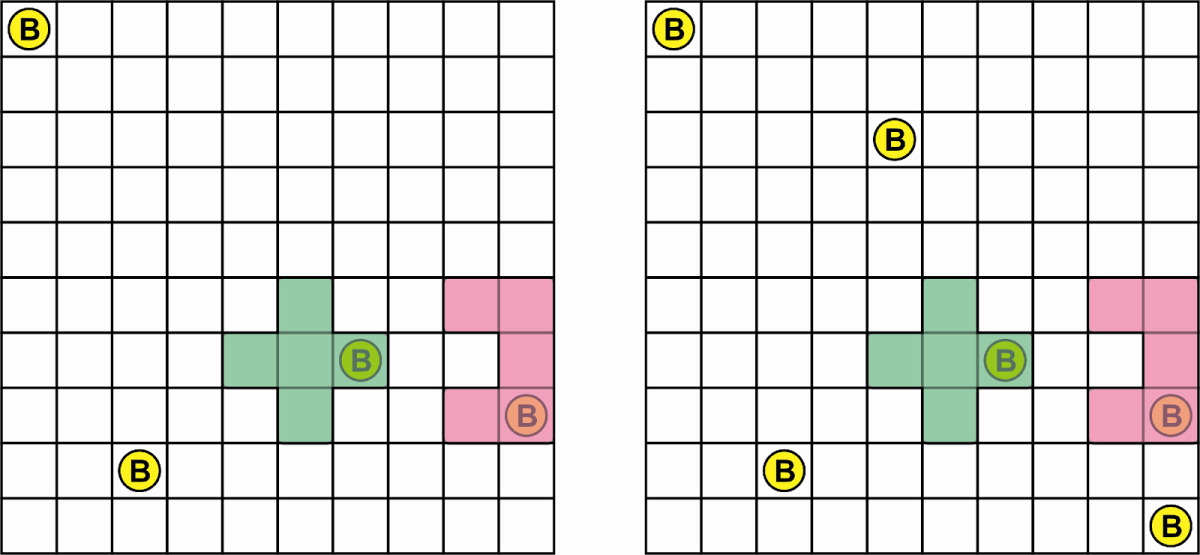
Figure 6: Claire draws her harvester collecting 1 coin, then draws two more coins
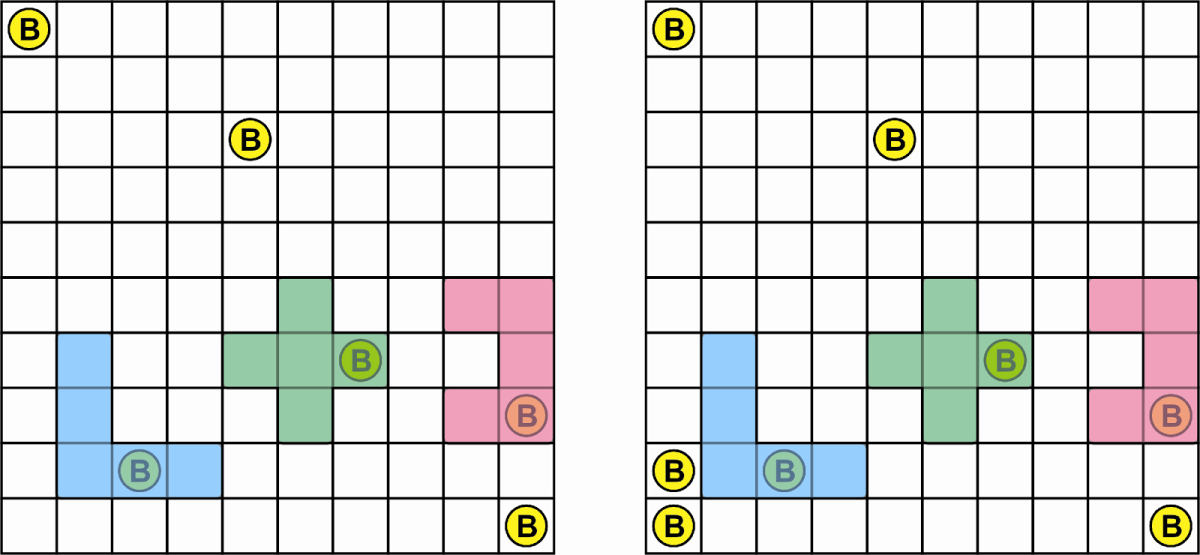
Figure 7: Ann cleverly draws her harvester (scoring another coin) and then draws 2 coins next to it, ensuring their capture on her next turn!
CHALLENGES
Here are a few puzzles for a single player. Use a single pentomino.
Challenge 1 (easy): Which pentomino is not capable of harvesting all these coins?

Figure 8: At least one pentomino is not capable of harvesting all these coins
Challenge 2 (medium): Which pentomino can harvest all the coins in figure 8 in the minimum number of turns? There can be several pentominoes that achieve the same result.
Challenge 3 (medium): Distribute 10 coins in a 8x8 grid so that the ‘L’ pentomino needs the maximum number of turns to harvest all of them (but no coin is left uncollected).
Please post your answers in my forum:
http://nestorgames.freeforums.org/bitcoin-magazine-puzzles-f16.html
... and I will reward the best post with a copy of one of my games. I’m looking forward to discussing your findings. Thank you for reading!
You might also enjoy my previous posts:
- Rise of the machines- Creativity as problem solving- The Bitcoin Maze










