I’m going to talk about the security behind Bitcoin addresses and keys, called Public Key Cryptography. This includes SHA256, Random Number Generators(RNGs), Hash Functions, and Elliptic Curve Digital Signatures (ECDSA.) If you have questions beyond this, please feel free to DM me. I am a mathematician by training, and I have a deep love for it. If you find that you have a new interest in cryptography as a hobby, there are many people who create cryptographic algorithms for fun, and their community can be helpful for your journey.
I promise that you only need some basic algebra for this, as well as a simple understanding of exponential functions. If you are familiar with modular arithmetic, that’s wonderful. If not,no biggie.
Cryptography has been around for thousands of years, and currently has a very robust community of professionals and hobbyists alike. The technology has come an extremely long way, and its current iterations allow for the online security which we hardly have to think about.
Let’s start with the concept of Public Key Cryptography, specifically within the context of Bitcoin. On the most basic level, PKC involves your private keys, and the public keys generated from them. PKC utilizes what are called “trapdoor functions” which are easy to solve (easy to generate a public key from a private key), but almost impossible to reverse engineer (find a private key given a public key.) This is due to the usage of modular arithmetic, exponential functions, and very large prime numbers.
Your bitcoin private keys are probably words, but they can also be a very large number. To be specific, when we begin the encryption, your private keys will be converted to a large number or binary string (series of ones and zeros) regardless of what its initial form was. How neat! This is why people sometimes say your private keys “represent a very, very large number” and is the reason for its security. While this is technically true in a deterministic/algorithmic sense, it’s not necessarily obvious why.
Private key generation is another interesting facet. Hardware and custodial wallets do this for you, and they may or may not tell you precisely how they go about it (open-source vs closed-source software.) This is definitely worth considering when choosing a wallet. The other option is to create your own from scratch. You can roll a good die, flip a coin or use some other similar method. There are also online random number generators which have been tested and graded by the professional cryptography community. RNGs frequently use the current time as their generator to create a small initial difference which, after enough iterations, makes a totally unique number. Choose an online RNG at your own risk. Even if the RNG itself is good, there may be malware on the site. The more you know!
So we have our secret words. Let’s see what happens next.
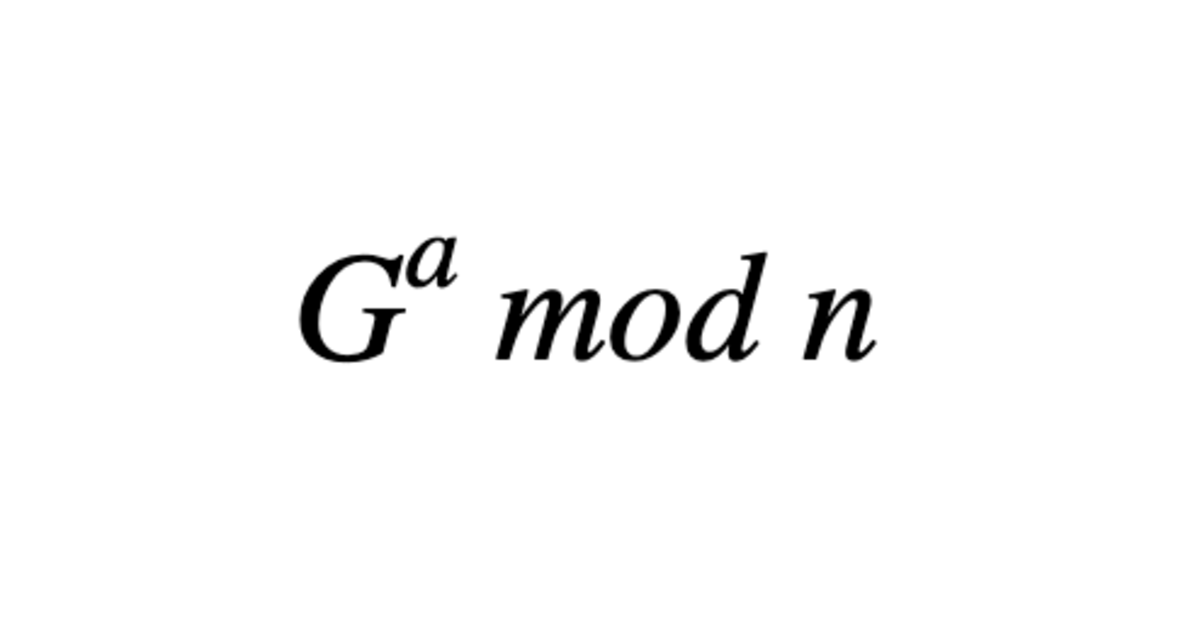
This is a very simple form of our trapdoor function. “G to the a mod n” represents our final public key (mod is short for modular arithmetic, which restricts our answer to a certain limit of numbers, as opposed to every single natural number). But, even if you know G and n, there’s no easy way for you to find a, which represents your private key. Calculating G to the mod n is relatively easy, but there’s no going backwards, thanks to the Discrete Log Problem. N is generally a large prime number because they are unfactorable by definition. Also, If relative complexities of functions/problems interest you, feel free to look into Algorithm Time Complexity.
Let’s go a little deeper, and look at it graphically for a more concrete understanding.
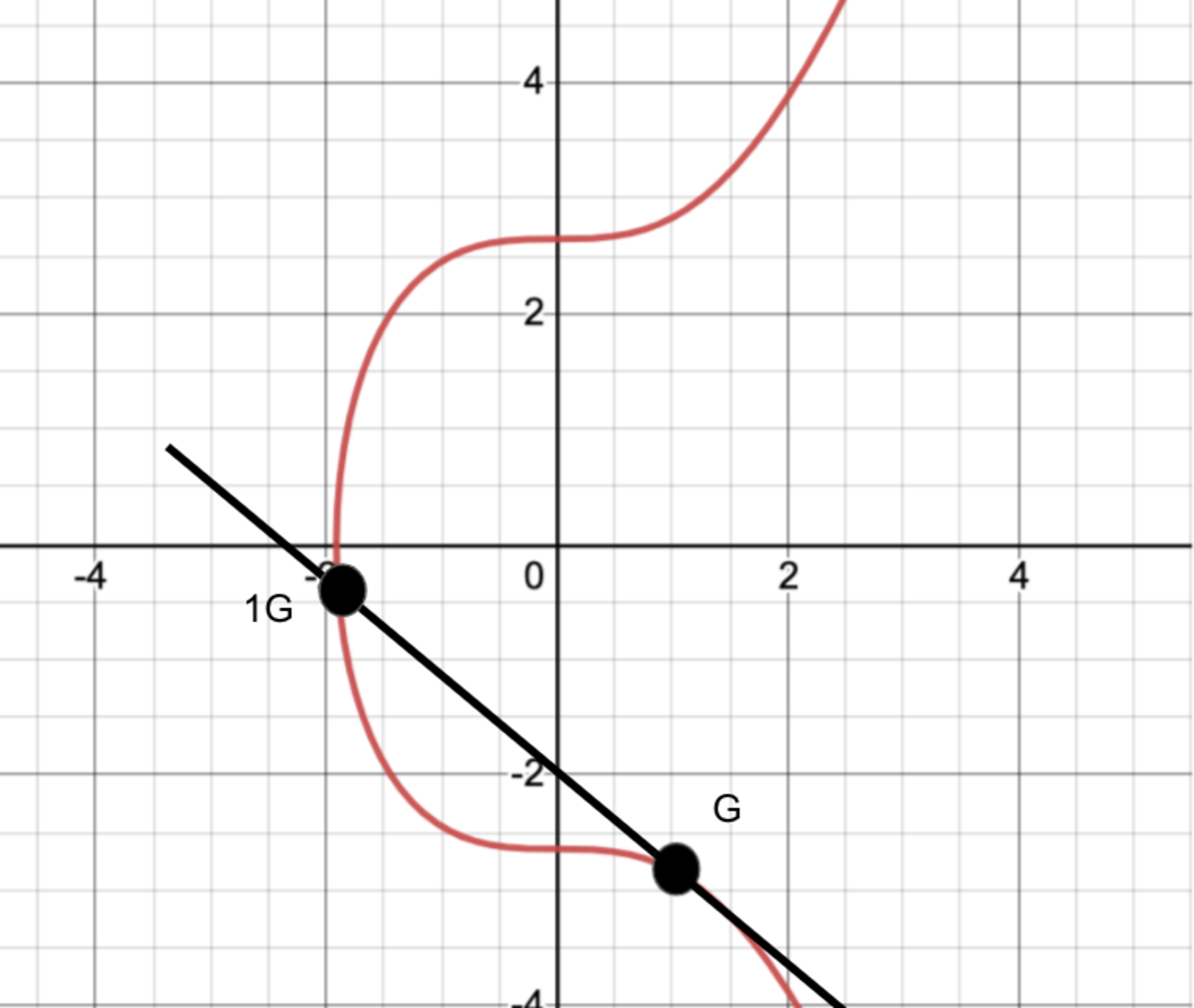
The red line is our curve, and is the specific one used by Bitcoin’s ECDSA. G is the point we start at, our “generator,” if you will. Then, we are going to “add” G to itself (although it isn’t addition in the usual sense - those crazy mathematicians love to redefine things. Don’t even get me started on topology!). In this case, adding it means we are going to take the tangent line of this point. Wherever that tangent line intersects the curve will be our next point. We will again take the tangent, and find a new point. In practice (on a computer) this is being done many thousands, or even millions, of times. The end result is that even if you know where I started, you don’t know how many times I “added” G to itself in order to get to the final point. How many times we performed the addition is your private key (your private number). Again, this is easy to check given a potential answer, but almost impossible to “brute force.” Voila!
So we have our first deterministic (one input gives you one answer) scrambling of information, but it’s not in a great format (right now, it’s just an ordered pair (x,y). We now have a public key, derived from a private one. Let’s scramble that information again and transform it.
We do this via SHA 256, which stands for Secure Hashing Algorithm. A Hashing Algorithm is a specific set of steps one applies to information, which results in an encrypted dataset of fixed length, regardless of the length of the input.
Yes, this family of algorithms was developed by the United States National Security Agency (NSA), but don’t let that worry you. The beauty of applied science — including mathematics, is that discovery and knowledge stand independent of who developed it. This is why we have proofs. If a proof is “sound,” then it stands on its own two feet, and cannot be “hacked” or worked around. The SHA2 family is public knowledge. You can go online and look at the code, and if you like use SHA256 yourself to encrypt some things. You’ll find that a very small change in input will have a dramatic output on the answer. Chaos Theory is beautiful. But anyhow.
As many people secure billions of dollars with SHA256, they have also spent a lot of money testing it to ensure its security. People frequently bring up quantum computing as a potential way to break this encryption. However, were quantum computing to become feasible, there is a lot more money to be stolen by hacking the top five major banks in the world. I’m sure Bitcoin is far down the list since, once it was hacked, its value would probably decrease dramatically. All that being said, if SHA256 becomes less secure in the future, we can always upgrade Bitcoin’s encryption methods. Programmable money!
SHA256 is similar to ECDSA in that it’s easy to check an answer, but very difficult to brute force — trying every answer until you find the right one. SHA256 is so named because it creates a string of 256 bits — a series of 256 zeros and ones. This makes for an absurdly high number of possible combinations, more than the number of atoms in the observable universe.
We are going to use a different hash again in order to get a smaller output, which makes for a shorter final address. This hash function is called RIPEMD-160. Once we have this result, we are going to convert it into what’s called Base58, which is just a form that’s more readable for humans.It omits both the number zero (0) and the uppercase letter O (o), so that they aren’t mistaken for each other, as well as omitting the uppercase letter I (i), so that it isn’t mistaken for the number one (1) or the lower case letter l (L) It omits both the number zero (0) and the uppercase letter O (o), so that they aren’t mistaken for each other, as well as omitting the uppercase letter I (i), so that it isn’t mistaken for the number one (1) or the lower case letter l (L).
And now we have a public address which is provably (in a formal, mathematical sense) created from a unique private address. Even if all seven billion people in the world create a new bitcoin public key every day for a thousand years, there are so many possibilities that the likelihood of creating the same one twice is almost zero.
All of this is quite the process, creating and verifying keys, hence our ten minute average block time. Ten minutes for mathematically-guaranteed final settlement is worth everything.
This is a guest post by Nameless. Opinions expressed are entirely their own and do not necessarily reflect those of BTC Inc. or Bitcoin Magazine.












